ENTREGA 3 - LÓGICA MATEMÁTICA II-2017

Posted on November 9, 2017 by Pedro Z.

ENTREGA 3  - LÓGICA MATEMÁTICA:

SI UN DOCUMENTO ENVIADO NO CUMPLE ALGUNA DE LAS SIGUIENTES PAUTAS, NO SERÁ RECIBIDO. DEBE CUMPLIR TODAS.

ENVIAR A MI EMAIL INSTITUCIONAL.

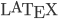  • UN sólo archivo pdf por cada grupo de 2 o 3 personas, en formato  \LaTeX.
  • En el cuerpo del email y en la primera página del pdf, especificar NOMBRE DE LOS ESTUDIANTES, CÓDIGO E EMAIL DE LA UNAL. DOCUMENTOS NO MARCADOS DENTRO DEL PDF NO SERÁN CALIFICADOS.
  • REENVIAR A TODOS LOS INTEGRANTES DEL GRUPO EN EL MISMO MOMENTO DE ENVIAR LA ENTREGA AL PROFESOR.
  • Enviar con asunto "ENTREGA 3 Lógica Matemática II-2017", hasta las 11:59 A.M.   del LUNES 13 DE NOVIEMBRE DE 2017. DOCUMENTOS ENVIADOS LUEGO DE ESA HORA NO SERÁN REVISADOS.
  1. Demuestre que si 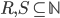R,S\subseteq \mathbb{N} son relaciones primitivas recursivas, entonces R\cup S es primitiva recursiva.
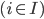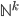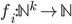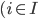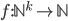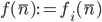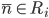  2. Demuestre que si R_i\subseteq \mathbb{N}^k (i\in I) son relaciones primitivas recursivas disyuntas dos a dos cuya unión es \mathbb{N}^k y f_i:\mathbb{N}^k\to \mathbb{N} ((i\in I) son funciones primitivas recursivas, la función f:\mathbb{N}^k\to \mathbb{N} definida por partes dada por f(\overline{n}):=f_i(\overline{n}) si \overline{n}\in R_i es primitiva recursiva.
  3. Demuestre que el conjunto 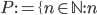P:=\{n\in \mathbb{N}: n es impar 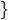\} es una relación primitiva recursiva.
  4. Demuestre que la relación 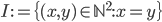I:=\{(x,y)\in \mathbb{N}^2:x=y\} es primitiva recursiva.
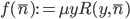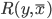  5. Demuestre que si f(\overline{n}):=\mu y R(y,\overline{n}) y R(y,\overline{x}) es un conjunto aritmético, demuestre que 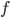f es una función aritmética.
This entry was posted in Logica Matematica II-2017. Bookmark the permalink.

Leave a Reply

Your email address will not be published. Required fields are marked *

You may use these HTML tags and attributes: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <strike> <strong>