Enviar un archivo pdf por persona en 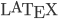 desde el email institucional HASTA LAS 11:59AM DEL MARTES 24 DE NOVIEMBRE DE 2015.
desde el email institucional HASTA LAS 11:59AM DEL MARTES 24 DE NOVIEMBRE DE 2015.
Enviar por email, con el asunto "Ejercicio 3 Teoría de Conjuntos".
(AC) Sea 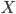 un conjunto no vacío. Decimos que
un conjunto no vacío. Decimos que 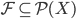 es un filtro sobre
es un filtro sobre 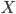 sii
sii
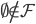
- Si
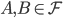 entonces
entonces 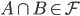
- Si
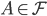 y
y 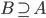 entonces
entonces 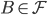
Demuestre que si 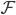 es un filtro sobre
es un filtro sobre 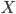 , entonces existe un filtro
, entonces existe un filtro 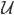
 -maximal que contiene a
-maximal que contiene a 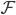 .
.
